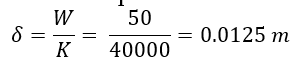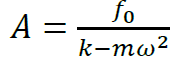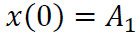La masa está sometida a una fuerza
armónica variable 𝐹(𝑡)=𝑓o𝑠𝑒𝑛
𝜔𝑡, donde
𝑓o es el
valor máximo de la fuerza impuesta al sistema y 𝜔 es el valor de la frecuencia con la cual varía, en radianes/segundo, la
fuerza 𝐹(𝑡).La ecuación diferencial adquiere la
forma: 𝑚𝑥̈+𝑘𝑥=𝑓o𝑠𝑒𝑛
𝜔𝑡 ; 𝑥̈(𝑡)+𝜔𝑛2𝑥(𝑡)=𝑓o𝑚cos(𝜔𝑡) y la solución general es la suma de
la solución homogénea y la solución particular, como se estudió en Ecuaciones
Diferenciales.
ecuación diferencial:
La solución homogénea tiene la forma:
𝑥𝑝(𝑡) solución particular
existen 3 casos, estos casos tienen que ver con la relación que existe entre la frecuencia natural del sistema y la frecuencia de excitación del sistema de la fuerza externa.
caso I: 𝜔≠𝜔𝑛
solución particular:
𝐴 es una constante
Donde 𝑟 es la relación de frecuencias
𝑑𝑒𝑓𝑙𝑒𝑥𝑐𝑖ó𝑛 𝑒𝑠𝑡á𝑡𝑖𝑐𝑎 en estado estable:
a) Si 𝜔 < 𝜔𝑛, la amplitud 𝐴 del movimiento forzado es positiva. La partícula 𝑚 y la fuerza exterior están en fase, y oscilan en el mismo sentido.
b) Si 𝜔 > 𝜔𝑛 , la amplitud 𝐴 del movimiento forzado es negativa. La partícula 𝑚 y la fuerza exterior están en desfase, y oscilan en sentido contrario.
donde cuando t=0:
CASO II 𝜔 = 𝜔𝑛 resonancia.
Si la frecuencia de la fuerza externa coincide con una de las frecuencias naturales del sistema,
ocurre una condición conocida como resonancia, y el sistema sufre oscilaciones peligrosamente
grandes. Las fallas de estructuras como edificios, puentes, turbinas y alas de avión se han asociado
a la ocurrencia de resonancia.
donde:
CASO III pulsaciones:Es importante observar que en estos sistemas se produce pulsaciones y suceden cuando la frecuencia de excitación tiene valores cercanos a la frecuencia natural. Si utilizamos la respuesta en el tiempo conocida.

ejemplo
tenemos una masa m=100kg que esta sometida vibraciones forzadas sin amortiguamiento el cual trabajaremos con los siguientes relaciones de frecuencia r=0.3, r = 1, r=1.2, con K=500 y fo=1 N N/m xo=0, vo=0 dibujar el desplazamiento de la masa respecto al tiempo para cada uno de los casos.
solución:
para estos casos utilizaremos un código en matlab para la facilidad de los cálculos los cuales se encuentra en a ultima parte de este documento
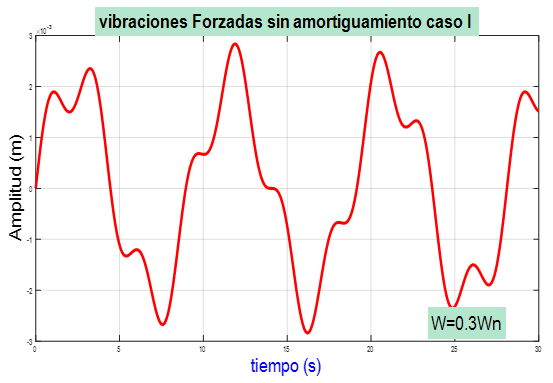
- con r = 0.3
- con r = 1
- con r=1.2
CÓDIGO MATLAB
clear; clc; close all
disp(' INGENIERÍA MECÁNICA - UNSAAC')
disp('-----------------------------------------------------------------------')
disp(' ')
disp(' curso:VIBRACIONES MECANICAS ')
disp(' tema: VIBRACIONES LIBRES
FORZADAS ')
disp('
')
disp('----------------------------------------------------------------------')
disp('
')
r=input('1) relacion de frecuencias r = ');
disp('
')
fo=input('2) el valor fuerza externa fo = ');
disp('
')
K=input('3) el valor del constante de
rigidez: K = ');
disp('
')
m=input('4) masa del cuerpo: m = ');
disp('
')
x_0=input('5) posicion inicial X_0
= ');
disp('
')
x_dot_0=input('6) velocidad inicial
inicial X_0_0 = ');
disp('
')
t=0:0.01:30;
Wn=sqrt(K/m);
W=r*Wn;
A=(fo/K)/(1-r^2);
Ar=-fo/(2*m*Wn);
B=(x_dot_0-A*W)/Wn;
B1=(x_dot_0-Ar)/Wn;
b=max(t)-max(t)/7;
if r~=1
Xt=x_0*cos(Wn*t)-B.*sin(Wn*t)+A*sin(W*t);
plot(t,Xt,'r','LineWidth',4)
title('vibraciones Forzadas sin
amortiguamiento caso I ','LineWidth',3,'Margin',6,'HorizontalAlignment','center','BackgroundColor',[.7 .9 .8],'FontSize',25)
xlabel('tiempo (s)','FontSize',25,'color','b')
ylabel('Amplitud (m)','FontSize',25,'color','k')
a=min(Xt)-min(Xt)/15;
text(b,a,['W=',num2str(r),'Wn'] ,'LineWidth',3,'Margin',6,'HorizontalAlignment','center','BackgroundColor',[.7 .9 .8],'FontSize',25)
else
Xt=x_0.*cos(Wn.*t)-B1.*sin(Wn*t)+Ar.*t.*cos(Wn.*t);
plot(t,Xt,'r','LineWidth',3)
a=min(Xt)-min(Xt)/15;
title('vibraciones Forzadas sin amortiguamiento caso II','LineWidth',3,'Margin',6,'HorizontalAlignment','center','BackgroundColor',[.7 .9 .8],'FontSize',25)
xlabel('tiempo (s)','FontSize',25,'color','b')
ylabel('Amplitud (m)','FontSize',25,'color','k')
text(b,a,['W=',num2str(r),'Wn'] ,'LineWidth',3,'Margin',6,'HorizontalAlignment','center','BackgroundColor',[.7 .9 .8],'FontSize',25)
end
grid on