VIBRACIONES FORZADA
introducción: Este fenómeno sucede cuando existe fuerzas exteriores aplicadas a un sistema vibratorio. Dicha fuerza exterior puede ser un simple impulso instantáneo, una oscilación mantenida, o incluso puede estar causada por fuerzas de inercia. Después de un cierto tiempo, la oscilación natural del sistema (régimen transitorio) desaparece por la presencia de fenómenos de resistencia, mientras que la oscilación estacionaria, debida a la fuerza exterior, tiene su misma frecuencia y perdura en el tiempo, Se consideran tanto sistemas amortiguados como no amortiguados. Luego, el factor de amplificación y los fenómenos de resonancia y batido se presentan en el contexto de un sistema de resorte-masa no amortiguado.
este fenómeno podemos expresarlo con el siguiente ecuación diferencial
este fenómeno podemos expresarlo con el siguiente ecuación diferencial

Ecuación de Movimiento: Sí
una fuerza f(𝑡)
actúa sobre un sistema masa-resorte amortiguador viscoso la ecuación de
movimiento puede ser obtenida usando la segunda ley de Newton o Lagrange, En vista de que esta ecuación es no uniforme, su solución general 𝑥(𝑡)esta dada por la suma de su solución homogénea, 𝑥ℎ(𝑡), y de la solución particular, 𝑥𝑝(𝑡).
vibración
armónica forzada sin amortiguamiento
La masa está sometida a una fuerza
armónica variable 𝐹(𝑡)=𝑓o𝑠𝑒𝑛
𝜔𝑡, donde
𝑓o es el
valor máximo de la fuerza impuesta al sistema y 𝜔 es el valor de la frecuencia con la cual varía, en radianes/segundo, la
fuerza 𝐹(𝑡).La ecuación diferencial adquiere la
forma: 𝑚𝑥̈+𝑘𝑥=𝑓o𝑠𝑒𝑛
𝜔𝑡 ; 𝑥̈(𝑡)+𝜔𝑛2𝑥(𝑡)=𝑓o𝑚cos(𝜔𝑡) y la solución general es la suma de
la solución homogénea y la solución particular, como se estudió en Ecuaciones
Diferenciales.
ecuación diferencial:
solución particular:

ecuación diferencial:
La solución homogénea tiene la forma:
𝑥𝑝(𝑡) solución particular
existen 3 casos, estos casos tienen que ver con la relación que existe entre la frecuencia natural del sistema y la frecuencia de excitación del sistema de la fuerza externa.
caso I: 𝜔≠𝜔𝑛
𝐴 es una constante
Donde 𝑟 es la relación de frecuencias
𝑑𝑒𝑓𝑙𝑒𝑥𝑐𝑖ó𝑛 𝑒𝑠𝑡á𝑡𝑖𝑐𝑎 en estado estable:
a) Si 𝜔 < 𝜔𝑛, la amplitud 𝐴 del movimiento forzado es positiva. La partícula 𝑚 y la fuerza exterior están en fase, y oscilan en el mismo sentido.
b) Si 𝜔 > 𝜔𝑛 , la amplitud 𝐴 del movimiento forzado es negativa. La partícula 𝑚 y la fuerza exterior están en desfase, y oscilan en sentido contrario.
donde cuando t=0:
CASO II 𝜔 = 𝜔𝑛 resonancia.
Si la frecuencia de la fuerza externa coincide con una de las frecuencias naturales del sistema,
ocurre una condición conocida como resonancia, y el sistema sufre oscilaciones peligrosamente
grandes. Las fallas de estructuras como edificios, puentes, turbinas y alas de avión se han asociado
a la ocurrencia de resonancia.
donde:
CASO III pulsaciones:Es importante observar que en estos sistemas se produce pulsaciones y suceden cuando la frecuencia de excitación tiene valores cercanos a la frecuencia natural. Si utilizamos la respuesta en el tiempo conocida.

ejemplo
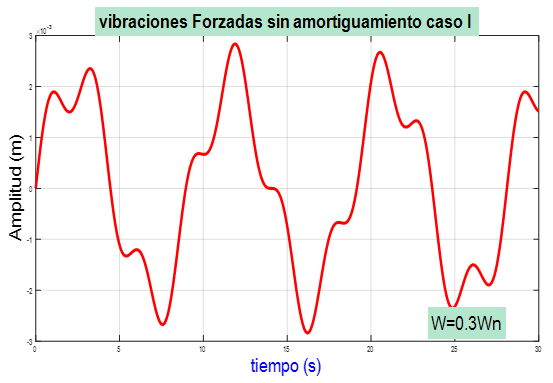
tenemos una masa m=100kg que esta sometida vibraciones forzadas sin amortiguamiento el cual trabajaremos con los siguientes relaciones de frecuencia r=0.3, r = 1, r=1.2, con K=500 y fo=1 N N/m xo=0, vo=0 dibujar el desplazamiento de la masa respecto al tiempo para cada uno de los casos.
solución:
para estos casos utilizaremos un código en matlab para la facilidad de los cálculos los cuales se encuentra en a ultima parte de este documento
- con r = 0.3
- con r = 1
- con r=1.2
CÓDIGO MATLAB
clear; clc; close all
disp(' INGENIERÍA MECÁNICA - UNSAAC')
disp('-----------------------------------------------------------------------')
disp(' ')
disp(' curso:VIBRACIONES MECANICAS ')
disp(' tema: VIBRACIONES LIBRES
FORZADAS ')
disp('
')
disp('----------------------------------------------------------------------')
disp('
')
r=input('1) relacion de frecuencias r = ');
disp('
')
fo=input('2) el valor fuerza externa fo = ');
disp('
')
K=input('3) el valor del constante de
rigidez: K = ');
disp('
')
m=input('4) masa del cuerpo: m = ');
disp('
')
x_0=input('5) posicion inicial X_0
= ');
disp('
')
x_dot_0=input('6) velocidad inicial
inicial X_0_0 = ');
disp('
')
t=0:0.01:30;
Wn=sqrt(K/m);
W=r*Wn;
A=(fo/K)/(1-r^2);
Ar=-fo/(2*m*Wn);
B=(x_dot_0-A*W)/Wn;
B1=(x_dot_0-Ar)/Wn;
b=max(t)-max(t)/7;
if r~=1
Xt=x_0*cos(Wn*t)-B.*sin(Wn*t)+A*sin(W*t);
plot(t,Xt,'r','LineWidth',4)
title('vibraciones Forzadas sin
amortiguamiento caso I ','LineWidth',3,'Margin',6,'HorizontalAlignment','center','BackgroundColor',[.7 .9 .8],'FontSize',25)
xlabel('tiempo (s)','FontSize',25,'color','b')
ylabel('Amplitud (m)','FontSize',25,'color','k')
a=min(Xt)-min(Xt)/15;
text(b,a,['W=',num2str(r),'Wn'] ,'LineWidth',3,'Margin',6,'HorizontalAlignment','center','BackgroundColor',[.7 .9 .8],'FontSize',25)
else
Xt=x_0.*cos(Wn.*t)-B1.*sin(Wn*t)+Ar.*t.*cos(Wn.*t);
plot(t,Xt,'r','LineWidth',3)
a=min(Xt)-min(Xt)/15;
title('vibraciones Forzadas sin amortiguamiento caso II','LineWidth',3,'Margin',6,'HorizontalAlignment','center','BackgroundColor',[.7 .9 .8],'FontSize',25)
xlabel('tiempo (s)','FontSize',25,'color','b')
ylabel('Amplitud (m)','FontSize',25,'color','k')
text(b,a,['W=',num2str(r),'Wn'] ,'LineWidth',3,'Margin',6,'HorizontalAlignment','center','BackgroundColor',[.7 .9 .8],'FontSize',25)
end
grid on




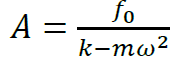


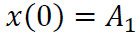








No hay comentarios:
Publicar un comentario